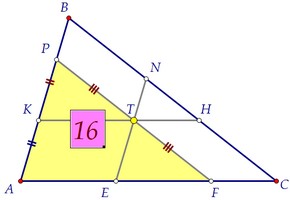
16 (С4). Знаейки областта на големи триъгълници, търси малка площ (вер. 83)
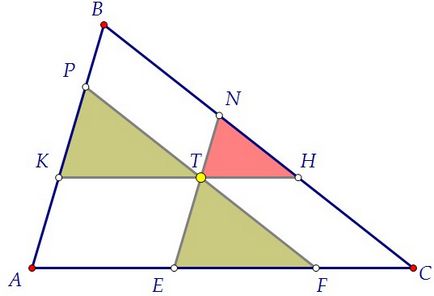
Чрез точка Т три права к проведе във вътрешността на триъгълника ABC, L и М, така че к || AB, л || BC, м || AC. Тези линии образуват триъгълник с три страни на триъгълник, две от които са равни по размер. а) докаже, че квадрата на сумата от квадратни корени на областите на триъгълници, образувани от прави линии, К, L и М на страните на триъгълника ABC. равна на площта на триъгълника; б) Намерете лицето на по-малкия триъгълник, ако е известно, че treug на областта. ABC е 25 и областта на всяка от еднакви триъгълници е 4.
Ясно е, че ако формулата на а) е доказано, да замени в данните й от б) не е трудно. Въпреки това взема самостоятелни решения б).
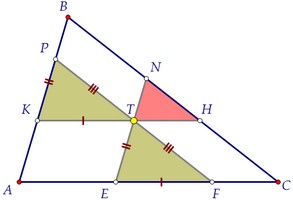
В триъгълници на фигура страни съответно успоредни една на друга. Лесно е да се докаже, че те са подобни в двата ъгъла. Ако областите на подобни триъгълници са равни, то триъгълниците самите също са равни (го докажа).
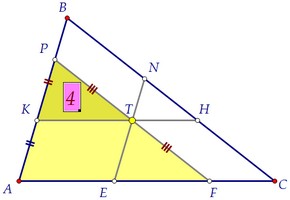
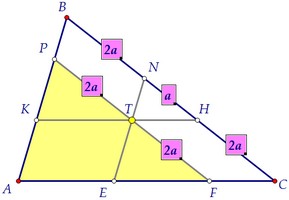
В равни триъгълници по дефиниция са равни на съответните страни. Днес празнуваме повече двойки равни страни, като се вземат предвид свойствата на успоредник. По този начин, CT - APF средната линия на триъгълника по дефиниция. APF площ на триъгълник е 4 пъти по-голяма от площта на триъгълника ABD. *** триъгълници с фактор на сходство на две.
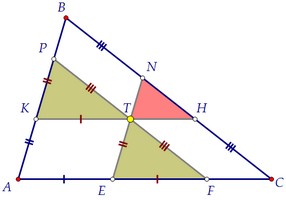
Триъгълниците APF и AVS също подобно. Техните площи са 16 и 25. Това означава, че съответните страни на триъгълници са както 4. 5. вземе предвид в същото време равнопоставеността на противоположни страни на успоредник:
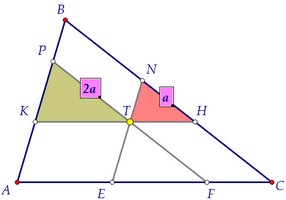
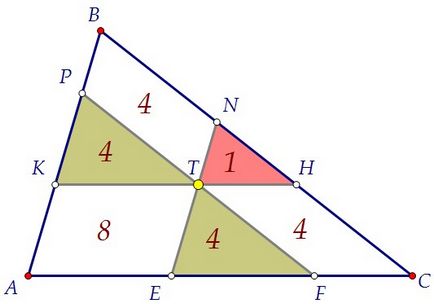
И накрая, ние се отбележи още един чифт подобни триъгълници: KPT и TNH. Коефициентът на сходство е равно на 2. Средната площ на загриженост, тъй като от 4 до 1. По този начин, в областта на малкия триъгълник TNH е 1. Отговор: 1
Докаже твърдение а) възможно, твърдейки, подобно определяне данни равни части по отношение на х. като се използва същият сходството и взаимоотношения. Но на следващата страница ще бъде доказано в общ вид. това е, произволна точка във вътрешността на триъгълника, наличието на не непременно равни триъгълници.