Как да се намери големината на вектора

Предишен ◈ Следващото

Вектор - геометрична обект, който се характеризира както от големината и посоката. [1] Големината на вектор е неговата дължина, и съответства на посоката, към която посочва. Големината на вектора се изчислява много лесно, за да направи няколко прости стъпки. Други важни операции с вектори включват добавяне и изваждане на вектори, намирането на ъгъла между двата вектора и изчисляването на вектор продукт.

стъпки Редактиране

Метод 1 от 2:
Изчисление на вектора, идващ от произхода Редактиране

Как да се намери големината на вектора

Как да се намери големината на вектора

Определяне на компонентите на вектора. Всеки вектор на самолета може да бъде числено представени в двумерен Декартова координатна система от две числа: хоризонтален (X ос) и вертикална компонента (у-ос). [2] Векторът може да бъде записано като двойка номера: V = .
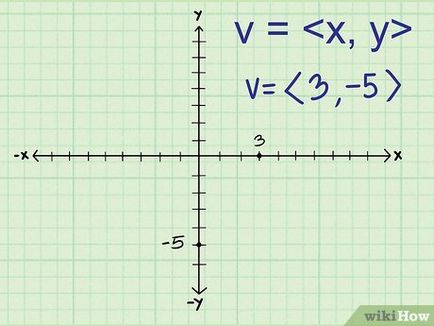
  • Например, ако хоризонталния компонент на вектора е равно на 3 и вертикалата е -5, този вектор се изписва като <3, -5>.

Как да се намери големината на вектора

Как да се намери големината на вектора

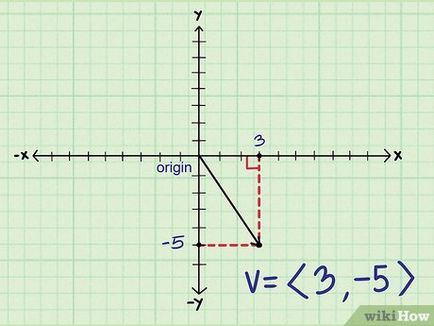
Начертайте вектор триъгълник. Ако сложите на хоризонтални и вертикални елементи, ще трябва правоъгълен триъгълник. Големината на вектора е дължината на хипотенузата на триъгълника, както и за неговото изчисляване, можете да използвате питагорова теорема.

Как да се намери големината на вектора

Как да се намери големината на вектора

За изчисляване на вектори, запишете питагорова теорема. Питагоровата теорема гласи, че сумата от квадратите на краката на правоъгълен триъгълник е равна на квадрата на неговото хипотенуза: A 2 + B 2 = С 2. В този случай, "А" и "В" - е хоризонталните и вертикалните компоненти вектор, и "С" представлява хипотенузата. Както хипотенузата е само вектор, е необходимо да се намери "C".
  • х 2 + Y 2 = о 2
  • V = √ (2 х + у 2))

Как да се намери големината на вектора

Как да се намери големината на вектора

Намерете най-вектор големината. За заместител в уравнение цифровите стойности, получени по-горе, т.е. съответните векторни компоненти.
  • В този пример V = √ ((от март 2 + (- 5) 2))
  • V = √ (25 + 9) = √34 = 5831
  • Не се заблуждавайте, ако резултатът не е цяло число. Дължината на вектора може да бъде фракционна стойност.

Метод 2 на 2:
Намирането на стойността на вектора, в началото на който не съвпада с произход Редактиране

Как да се намери големината на вектора

Как да се намери големината на вектора

Определя координати на началото и края на вектора. Всеки вектор на самолета може да бъде числено представени в двумерен Декартова координатна система от две числа: хоризонтален (X ос) и вертикална компонента (у-ос). [3] Векторът може да бъде записано като двойка номера: V = . Ако в началото на вектора не съвпада с началото на декартова координатна система, е необходимо да се определят координатите на точка на вектора на начало и край.
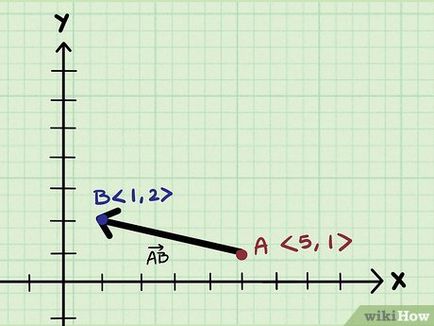
  • Нека вектор AB свързващи точки А и В.
  • Точка е хоризонтална координира и вертикалната координата на 5 1, така че координатите могат да бъдат изразени като двойки номера <5, 1>.
  • Точка В има хоризонтална координира и вертикалната координата 1 2, поради нейните координати могат да бъдат изразени като двойки номера <1, 2>.

Как да се намери големината на вектора

Как да се намери големината на вектора

За големината на вектора, като се използва модифицирана формула. Тъй като в този случай дава координатите на две точки се изважда координатите х и у на една точка на съответните координати на втората точка: V = √ ((х2 -Х1) 2 + (y2 -Y1) 2). [4]
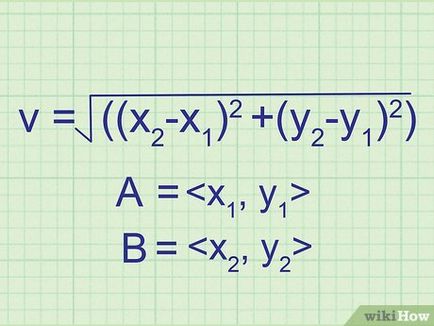
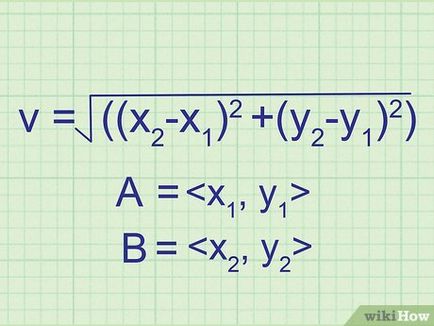
  • Нека точка А има координати , и буква б - координати

Как да се намери големината на вектора

Как да се намери големината на вектора

Намерете най-вектор големината. Сложете на координатите на точките в уравнението и да се изчисли дължината на вектора. В този пример изчисление е, както следва:
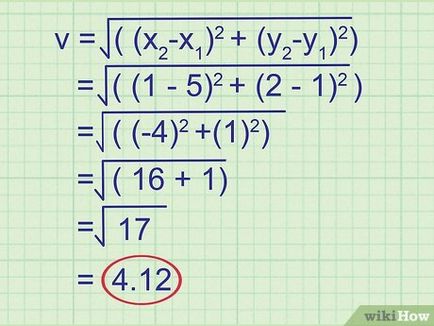
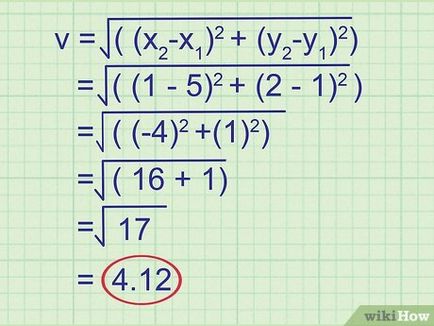
  • V = √ ((х2 -Х1) 2 + (y2 -Y1) 2)
  • V = √ ((1-5) 2 + (2-1) 2)
  • V = √ ((- 4) 2 + (1) 2)
  • V = √ (16 + 1) = √ (17) = 4.12
  • Не се заблуждавайте, ако резултатът не е цяло число. Дължината на вектора може да бъде фракционна стойност.
Предишен ◈ Следващото