максималните и минималните стойности на функции в интервал
Добър ден на всички мои скъпи читатели!
В тази статия ще се опитаме да се научите как да се определят максимални и минимални стойности на различните функции на прости и по-сложни, намирането на екстремалната точки, за да се определи дали минимум крайната стойност или максимални функции, и дори отличават инфлексна функцията на крайност.
ние действаме, както следва:
1. Определяне на производно на функцията.
2. Приравняването на производно на нула за да се определи дали екстремумите на функцията е (ако получената уравнението корени). Ще се определи дали данните принадлежат към крайностите на зададения интервал.
3. Ако функцията има екстремум в предварително определен интервал от време, определя дали е висока или ниска.
4. Ако функцията не екстремум (няма корени от уравнения, получени чрез равнява на производно на нула), определяне на знака на производно. Това ще ни покаже дали или не на функцията за увеличаване или намаляване. След това се процедира за състоянието на проблема: При увеличение на функция, максималната стойност на дясната страна, а минималната - на ляво. Ако намалява - напротив. решаване на проблеми ще помогне на всички нас, за да сортирате чрез и с помощта на снимки, ние ще се опитаме да не напускат мрачните места в решаването на такива проблеми.
Задача 1. Необходимо е да се определи най-голямата стойност на функцията:
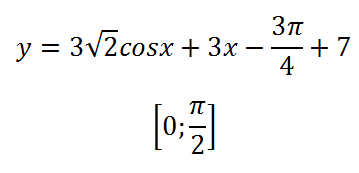
Ние работим в съответствие с алгоритъма, първо определете деривата. Тук имаме сумата от функции, така че ние определяме производната на всеки поотделно и да добавите до и след това се равнява на производната на нула:
Ние решаваме полученото уравнение. Ако корените са - след това, може би, имаме крайности (точката, където производното е нула, не може да бъде екстремум, и инфлексната точка).
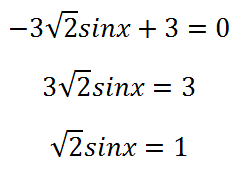
Ние виждаме - корен е:
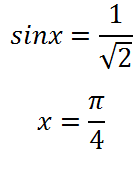
В този момент, нашата функция е екстремна. Важно е, че този въпрос принадлежи на определен интервал от време. Разберете най-този или minimum.Dlya тя трябва да определи знака на производната в околностите на този етап, това е, отдясно и отляво на него. Например, можете да вземете точка - това е от лявата страна, и точката, - тя ще бъде прав. След това:
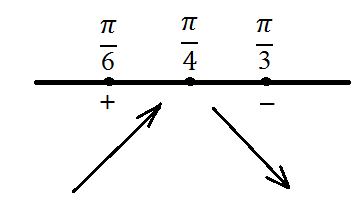
Ясно е, че функцията е с максимална стойност в точка maksimuma.Naydem тази стойност, както следва: Замяната на точката на екстремалната функция в уравнение:
A: най-голямата стойност на функцията в даден интервал е 10.
2.Find малката стойност на функцията на специфициран интервал:
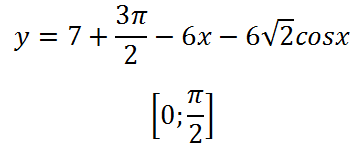
По същия начин, както и за първи път, ние приемаме производната и се нулира:
Вече е ясно, че това уравнение има корени:
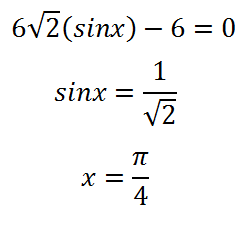
На мястото, на функцията е екстремна. Максимална или минимална е? Нека да се намери стойността на деривата в дясно и в ляво от точката. Отново, ние приемаме една точка - той ще се намира в ляво, и точката, - тя ще бъде прав. След това:
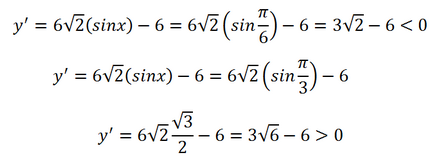
Функция отнема най-малката стойност в точка м inimuma на, ние го намерите:
Отговор: Минималната стойност на функцията в този интервал е 1.
Нека да решим следния проблем:
3. Определяне на най-голямата стойност на интервала:
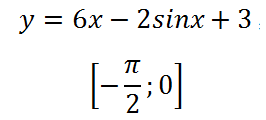
На първо място, както винаги, производна:
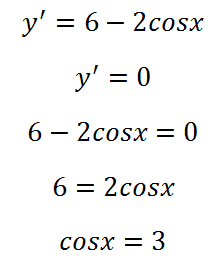
Такъв е случаят, когато екстремумите на функцията в този интервал е: в горното уравнение все още няма корени. Това означава, че функцията е монотонна или намалява или увеличава. Ние можем да се определи това, като знака на производната ако производната е положителна - функцията се увеличава, ако е отрицателно - намалява. Защо ние трябва да знаем функцията увеличава или намалява? Факт е, че ако функцията увеличава, стойността му винаги ще бъде по-голям от десния край на интервала, и намалява, ако - в ляво.
В нашата страна, без значение какъв ъгъл вземем, защото тя е по-малко от 1, така че производната е положителен, което означава, че функцията се увеличава. Така максималната си стойност достига точката 0:
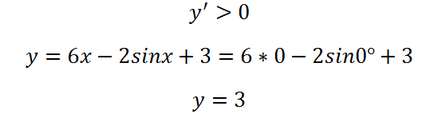
4. Определяне на минималната стойност на функцията на сегмента:
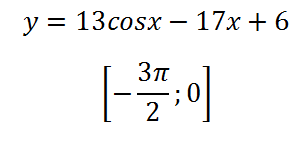
Ние дефинираме производно и се равняват на нула:
Вече е ясно, че функцията е монотонно (няма корени на получената уравнението):
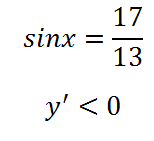
Тъй като производната е отрицателен, тогава ние заключаваме, че функцията намалява. Тогава най-ниската си стойност - в десния край на сегмента, т.е. 0:
Отговор: Минималната стойност на функцията на определен интервал от време - 19.
5. Намерете най-малката стойност на функцията на сегмента:
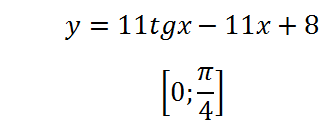
Обърнете производно се равняват на нула и решаване на получената уравнение:
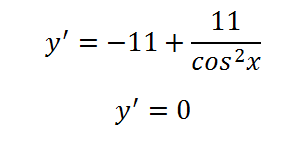
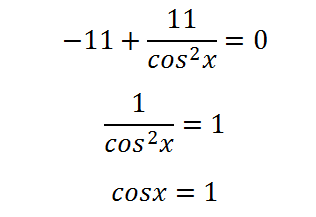
Тя ще изглежда - уравнението има корени, така че функцията ще има изключителна стойност в този сегмент (вторият коренът на този сегмент не принадлежи, така че не се счита). Определяне на максимална или минимална е. При стойност 1 за косинус - максимумът, който е някакъв момент или да се близо до нулата - косинус - абсциса - ще бъде по-малко от най-нула. Въпреки това! Производни нула цяло и марки не се променя! Положително е, в съседство на нула, а след това се увеличава, като функция на нула, а след това. Така че, на функцията в точката на нулата не екстремум и инфлексия.
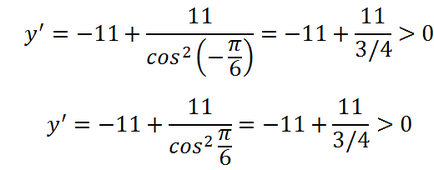
Ето защо, за да се определи най-ниската стойност, трябва да се вземе ляв край на сегмента и броя на стойността на функцията в тази точка. По щастливо стечение на обстоятелствата тази нулева точка. Въпреки това, той може да е друга точка, различна от нула, а след това бихме могли да допуснете грешка, като се има предвид нулевата точка на екстремум, и определяне на стойността на дадена функция в нея. По този начин стойността на функцията:
Отговор: Минималната стойност на функцията на определен интервал от време - 8.
6. Намерете точката на максимална функция:
Алгоритъмът изпълнението на такива функции са еднакви. На първо място - на деривата. Тук имаме произведение на две функции, така че ние се производната на правилото за вземане на производната на характеристиките на продукта:
Освен това се равнява на този израз на нула. Ясно е, че експонентата винаги е неотрицателна, в някаква степен или изграждат, така че коренът на "скрития" във втория фактор:
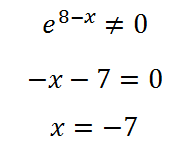
Уверете се, че този екстремум - максимум. Наистина, в този момент производните промените знак, и промени от положителен към отрицателен, а именно до този момент се увеличава функцията и след - намалява.
7. Намерете най-малката стойност на функцията на сегмента:
Ние ще, както обикновено, да се намери производната на тази функция, както и тази функция е сложна: (! И степен - дори и да я накара да подпише дневника, е необходимо да се постави модула знак, така че да не се стесни дефиницията на функцията) логаритъм изразена в градуси. Следователно, за да не разкрива модула, можем да използваме правилото на вземане на производно на съставна функция:
Получената експресията е определено равно на нула:
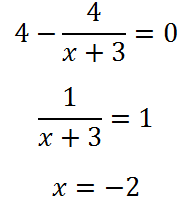
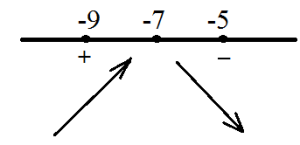
Имайте предвид, че точка (3) производно не е дефинирана. Въпреки това, в този момент да подпишат деривативните промените. Точка (-2) - минимум функция, тъй като деривати промени знак отрицателно на положителна. Следователно, в този момент минималната стойност на функция. Намерете го:
Отговор: Минималната стойност на функцията на определен интервал от време - 8.
8. Намерете точката на максимална функция:
Ние определи производно на съставна функция. Намерено равнява на производно на нула:
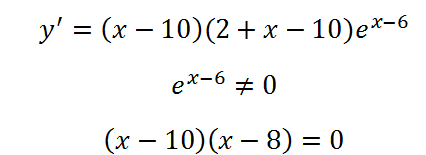
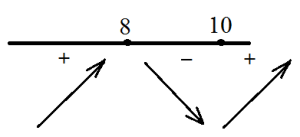
Имаме две точки на крайности. Един от тях - максимумът, а другият - най-малко.
Функция има максимален при 8.
9. Намерете най-ниската точка на функцията:
Определя производни, в допълнение, експонентата е сложна функция (тук, производното на степента, до която повишени експонентата е равно на 1). Намерено равнява на производно на нула:
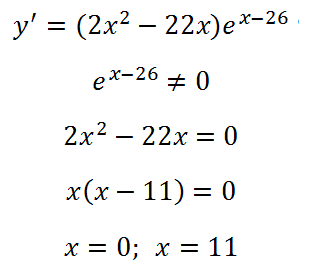
Минималната точка на функцията е точката, 11. Това може да се види: производната в това променя подпише от минус до плюс.
Отговор: х = 11.
10. Намерете най-ниската точка и максимума на функцията:
Ние определи производно на съставна функция. Намерено равнява на производно на нула:
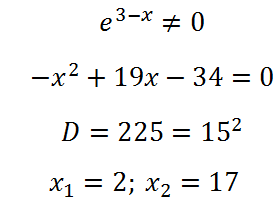
Производното на тази функция се променя знак от отрицателна на положителна в точка 2 (минимум) и от положителната към отрицателната - на 17 (максимум).
11. Намерете най-малката стойност на функцията на сегмента:
Трябва да отбележим, че изразът под логаритъм е по-голяма от нула. След 0 "заглавие =" х + 3> 0 "/> [/ pmath] -3" заглавие = "х> -3" /> [/ pmath]. Сегмент, на която ще се разгледа и определи функцията на деривативни признаци отговаря домейн на функцията.
Нека да намерим производната и се равняват на нула:
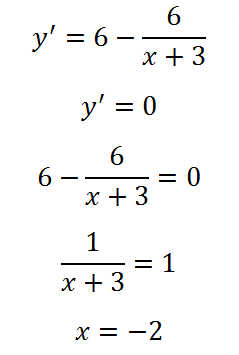
В точка 2, производните промени влизат, то тогава е крайно. Той се променя знак от отрицателни към положителни, така че тази точка - минималния точка. Това отнема най-малката стойност на функцията:
Отговор: Минималната стойност на функцията на определен интервал от време - 8.
12. Намерете най-малката стойност на функцията на сегмента:
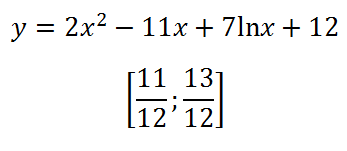
Нека да намерим производната и се равняват на нула:
Може да се отбележи, че функция домейн - положителни стойности на х (като израз на логаритъма по-голяма от нула), и че производното в точката 0 не е opredelena.Poluchim квадратното уравнение, в което сумата на коефициентите равни на 0 (A + B + C = 0) , В това уравнение, един корен е 1 и втория в / а:
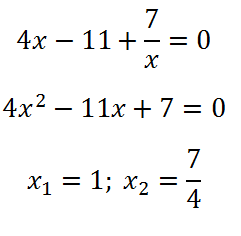
Задайте сегмент притежание само на една точка - 1. производно тук променя знак от отрицателни към положителни, и по този начин, то е минимално. Ние определяме стойността на функцията в този момент:
13. Намерете най-малката стойност на функцията на сегмента:
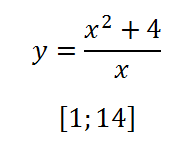
Имайте предвид, че функцията не е дефинирана в точката 0.
Ние приемаме производното на фракцията:
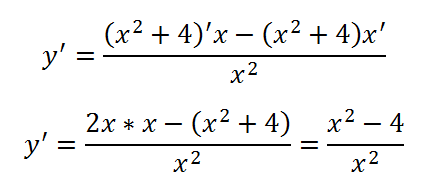
Ние приравняваме производна на нула, а ние търсим корените:
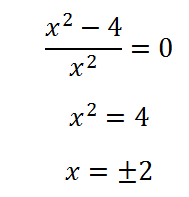
Един от корените не ни интересува, защото разликата не принадлежи на, а втората точка на деривативни промени подпише от негативна на polozhitelnyy.To функция има минимален в този момент. Определяне на минималната си стойност: