Пълното проучване на функцията и интригите - studopediya

Пълно изследване на функциите и техните строителни графици удобни за извършване, както следва:

1), за да намери площ определение функция;

2) определя дали функцията не е равна или нечетен, периодично;

3) за разследване на приемственост, да се намери равновесна точка и изясняване на естеството на прекъсвания;

4), за да открие асимптота на графиката;

5) проучи монотонността на функцията и да намерят своите крайности;

6) Виж инфлексната точка, определени интервали на изпъкналост и вдлъбнатина на графиката на функцията;

7) означава графиката на допълнителни точки, например неговото пресичане точка с координатните оси.

Резултатът от всяка точка трябва да се отрази веднага на графика и да бъде в съответствие с резултатите от изследванията на предходните алинеи.

За провеждане на цялостно изследване на функцията и начертайте графиката.

1. Функцията определено в х интервалÎ (- ¥ 1) È (-1 + ¥).

2. Функцията не може да бъде още по-странно, или, тъй като потребителите на дефиниция не е симетрична по отношение на 0. Ето защо, функцията на обща форма, т.е. Паритет не притежава имущество. Също така, функцията не е периодична.

Функцията се нарича още. ако са изпълнени следните две условия:

а) своя домейн на определение е симетрична по отношение на нула,

б) за всички стойности на х в областта на равенството.

Графика дори функция има аксиална симетрия около оста OY.

Функцията се нарича странно. ако

а) своя домейн от функцията е симетрична по отношение на нула,

б) когато "х в областта на дефиниция.

Графика странно функция има централна симетрия по отношение на произхода.

Функцията се нарича периодична. ако има редица T> 0 е такова, че равенството на "х в областта на дефиниция.

Броят Т е периода на функцията. и графика, е достатъчно да се изгради във всеки интервал на дължина Т. и след това периодично обхване цялата област.

3. Функцията е непрекъсната за всички хÎ (- ¥; -1) È (-1 + ¥).

Тази функция е единица, която се образува чрез разделяне на две непрекъснатост и основния елементарен. Поради това, свойствата на непрекъснатост, тази функция е непрекъсната във всички точки, на което се определят.

X = -1 е точката на счупване, тъй в него, това не е дефинирана функция. За да се определи характера (типа) на пропастта, изчисли. Следователно, за х = -1 функция е безкраен прекъсване (II празнина род).

4. асимптота на функциите на графиката.

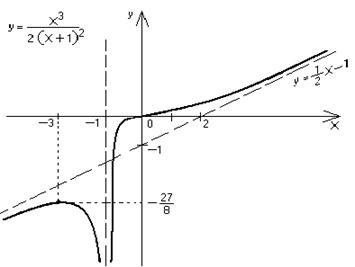
Вертикална асимптота е линията х = 1 (това следва от счупване изследвания функция).

Наклонени асимптота търсят уравнение. където

Така, - това уравнение наклонена асимптоти (в h® ± ¥).

5. монотонността и крайности определят функцията с помощта на първото си производни:

Критичната точка се определя от следните условия:

Достатъчни условия на монотонност и екстремумите:

6. интервали от изпъкналост и вдлъбнатина на графиката на функция, неговата инфлексна точка се използват втората производна:

Подозрителен в инфлексната точка се определя от следните условия:

Достатъчни условия за изпъкналостите, вдлъбнатина и инфлексия точки:

Точка О (0, 0) е инфлексна точка на графиката.

резултати от изследвания често функционират с помощта на първата и втората производна изготви обща таблица, която показва основните свойства на графиката на функцията:

Всички резултати от изследвания функция отразява своята програма.

OOF: хÎ (- ¥ -) È (-) È (+ ¥).

Това е странно, функция, тъй като потребителите са симетрични по отношение на нула и "х Î OOF равенство:

Следователно, графиката на функцията има централна симетрия спрямо произхода.

Функцията е непрекъсната за всички хÎ (- ¥ -) È (-) È (+ ¥), като елементарна функция е непрекъсната по своя OOF. X = - = и х са точки на безкраен прекъсване, тъй

Вертикална асимптота на графиката са линии X = - и X =.

Наклонена асимптота :. където

- това уравнение наклонена асимптота.

Интервали от увеличаване и намаляване на функцията, неговите крайности.

Предварителни Extrema:

Достатъчни условия на монотонност и екстремумите:

Интервалите на изпъкналост, вдлъбнатина на графиката на функцията и инфлексната точка:

х на точката = 0 на инфлексия подозрителен.

Точка О (0, 0) е инфлексната точка.

Цялата маса от основните свойства на графиката за тази функция може да се създаде само за хÎ [0; + ¥) като следствие от централната симетрия по отношение на графика точка (0, 0):